Drapieżniki i ofiary: model Lotki–Volterry

Historycznie pierwszym formalnym opisem oddziaływania dwóch populacji w ekosystemie jest model Lotki–Volterry. Dotyczy on układu drapieżnik–ofiara: populacja drapieżników żywi się osobnikami gatunku ofiary. Model został zaproponowany w latach dwudziestych ubiegłego wieku równolegle przez Vito Volterrę jako model populacyjny oraz przez Alfreda Lotkę jako model łańcucha reakcji chemicznych. Volterra zaproponował ten model w celu wyjaśnienia zjawiska, które zostało zaobserwowane po I wojnie światowej. Zauważono, że populacja ryb drapieżnych w Morzu Adriatyckim zwiększyła się. Uznano to za paradoks, gdyż zdawałoby się, że wszystkie gatunki powinny ucierpieć w wyniku działań wojennych. Volterra na bazie swojego modelu wykazał, że wzrost liczebności drapieżników był naturalny, ponieważ w czasie wojny zaprzestano połowów i dzięki temu populacja drapieżników mogła wrócić do swego stanu naturalnego.

Model przyjmuje następujące założenia:

• W środowisku występują tylko dwa gatunki: ofiar i drapieżników.
• Jeżeli w środowisku nie ma drapieżników, to ofiary mają sprzyjające warunki (tzn. nie ma żadnych dodatkowych ograniczeń środowiska) i ich populacja wzrasta wykładniczo (czyli zgodnie z prostym modelem Malthusa).
• Jeżeli w środowisku nie ma ofiar, to drapieżniki nie maja pożywienia, co wiąże się z brakiem energii niezbędnego do przeżycia i rozmnażania, co skutkuje wymieraniem gatunku (liczebność populacji maleje wykładniczo).
• Kiedy oba gatunki występują w środowisku, część ofiar ginie upolowana przez drapieżniki. Pożywienie dostarcza drapieżnikom energii niezbędnej m.in. do rozmnażania, a zatem liczebność ich populacji rośnie.
• Polowanie jest możliwe tylko w przypadku bezpośredniego kontaktu, osobniki poruszają się losowo, zatem liczba kontaktów jest proporcjonalna do liczebności obu gatunków.
• Rozmieszczenie osobników w środowisku nie jest uwzględniane. Rozważamy tylko średnie zagęszczenie osobników.

Symulacja modelu Lotki–Volterry

Wybierz język programu:

Opis programu

Powyższa wieloagentowa symulacja jest inspirowana modelem Lotki–Volterry. Symulacja nie jest idealnym odpowiednikiem modelu: model ma naturę ciągłą, a poza tym symulacja uwzględnia położenie osobników w środowisku. W rozważanym modelu oddziałują na siebie dwa gatunki: ofiary (króliki) oraz drapieżniki (lisy). Jednostki poruszają się w sposób losowy i są wizualizowane przez kolor zielony oraz czerwony.

Domyślne parametry pozwalają zaobserwować oscylację liczności parametrów populacji królików i lisów. Można to wytłumaczyć w prosty sposób: zwiększenie liczby królików powoduje po niewielkim czasie wzrost liczby lisów. Populacja rozwija się dzięki dostępności pożywienia. Jednak po pewnym czasie zabraknie pożywienia dla całej populacji lisów, przez co lisy będą wymierały. Z kolei to wpłynie na odrodzenie populacji królików i cały cykl rozpocznie się od początku.

Liczebność oraz zmienność w czasie (tj. dynamikę populacji) można zaobserwować na wykresach. Pierwszy przedstawia tzw. portret fazowy układu równań. Osie układu współrzędnych odpowiadają liczności populacji obu gatunków, a zaznaczone punkty opisują wzajemnie powiązane wielkości populacji dla kilku ostatnich kroków symulacji. Drugi wykres przedstawia zależność liczby osobników każdego gatunków w zależności od czasu (co ma związek z rozwiązaniem układu równań modelu L-V – czytaj niżej). Osie opisujące wielkości populacji mają jednostki odnoszące się do części środowiska zajętej przez ich osobników, np. 50% oznacza, że połowa środowiska zajęta jest przez daną populację.

Wskazówki dotyczące użytkowania programu:

Parametry symulacji

• Rozmiar świata określa rozmiar środowiska symulacji.
• Pocz. % Królików i Pocz. % Lisów odnoszą się do początkowych procentowych zajętości populacji w środowisku.
• P(K Rozmnażanie) jest odpowiednikiem parametru r z układu L-V opisanego poniżej.
• P(L Rozmnażanie) jest odpowiednikiem parametru b z układu L-V.
• P(L Śmiertelność) jest odpowiednikiem parametru s z układu L-V.
• P(L Skuteczność) jest odpowiednikiem parametru a z układu L-V.

Parametry będące odpowiednikami z układu równań L-V interpretowane są jako prawdopodobieństwa zajścia odpowiednich zdarzeń w kolejnych iteracjach symulacji. Warto poeksperymentować z parametrami podczas trwania symulacji, aby zaobserwować, jak wpływają na zmiany rozmiarów obu populacji królików i listów. Możesz spróbować tak dobrać współczynniki, aby doprowadzić do wyginięcia jednej z populacji.

Uruchomienie symulacji

Przycisk Start rozpoczyna symulację. Szybkość symulacji można kontrolować odpowiednim suwakiem. W trakcie działania symulacji możliwa jest zmiana niektórych parametrów, a ich wpływ na ekosystem można obserwować na żywo na wizualizacji środowiska i wykresach. Przycisk Reset powoduje losową inicjalizację środowiska z uwzględnieniem wartości Rozmiar świata, % Królików i % Lisów.

Teoria

Oznaczmy przez

V(t) – liczebność (zagęszczenie) ofiar w chwili t;
P(t) – liczebność (zagęszczenie) drapieżników w chwili t.

Układ równań wraz z podanymi powyżej założeniami nazywamy modelem Lotki–Volterry (L-V) lub modelem drapieżnik–ofiara (dla uproszczenia pominięto zmienną niezależną t)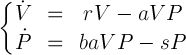

gdzie

• r jest współczynnikiem rozrodczości gatunku ofiar;
• aVP oznacza biomasę upolowanych ofiar, przy czym a jest współczynnikiem skuteczności polowań, czyli określa, jaka cześć spotkań drapieżników z ofiarami kończy się jej upolowaniem;
• b oznacza cześć energii uzyskanej z polowania przeznaczonej przez drapieżniki w procesie rozmnażania (tzw. przeliczniki biomasy upolowanych ofiar);
• s jest współczynnikiem śmiertelności gatunku drapieżników.

Okazuje się, że dla nieujemnych danych początkowych istnieją rozwiązania układu, które są jednoznaczne i nieujemne (mają zatem sens biologiczny). Rozwiązaniem układu są funkcje okresowe przesunięte w fazie.

Literatura

Urszula Foryś, Matematyka w biologii, Warszawa 2005, WNT.

Program i tekst: Łukasz Idkowiak

Przetłumaczenie na javascript: Magdalena Waligórska

Opiekun: Maciej Komosinski